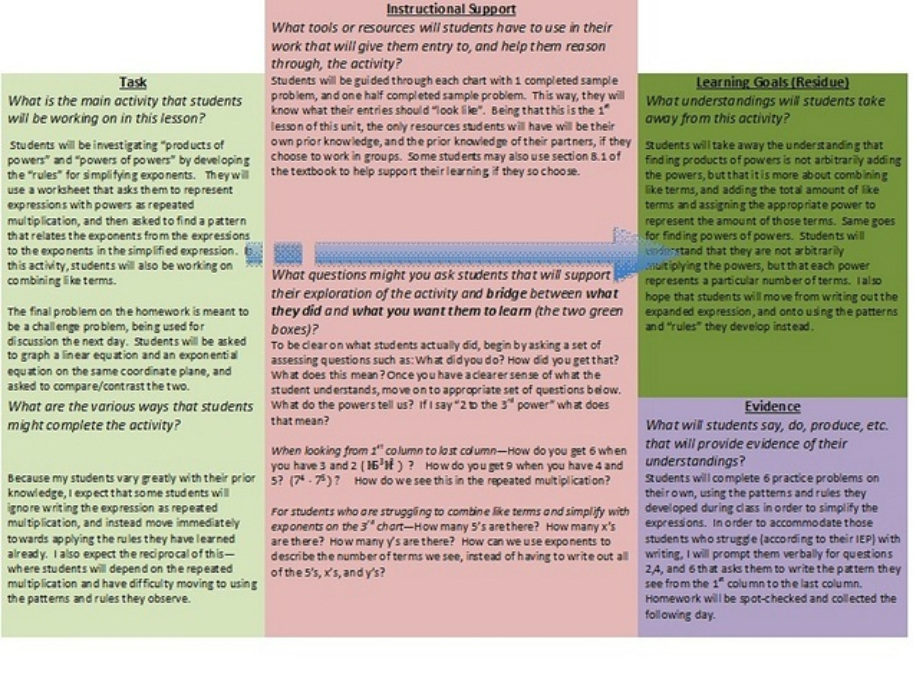
Engaging Students by Finding Patterns in Exponents
This is the first lesson of the new unit focusing on exponents and exponential functions. I knew that I wanted my students to develop the patterns for properties of exponents on their own, versus me telling them to either "add, multiply, or subtract" the powers in given situations. I felt that, before this unit, my students had a very poor understanding of what the power of a term meant. Many of my students, for example, confused 3^2 to mean 3*2, instead of 3*3. Therefore, I wanted to address these misconceptions by having the students write each expression as repeated multiplication, showing them what was really going on in the expressions. I also wanted my students to be engaged in the development of the "rules" for multiplication properties of exponents, rather than simply being told what to do and what the rules are. This lesson also begins the unit of assignments and classwork that I am experimenting on not using the book at all. I have noticed in previous lessons that the likelihood a student will complete an assignment increases if this is on a worksheet, versus work out of the book. Therefore, this lesson sets the groundwork for the rest of the unit, and the format of assignments to follow.
| orielly_8.1_multiplication_properties_of_exponents_worksheet.docx | |
| File Size: | 19 kb |
| File Type: | docx |
| cs3_8.1_lpe_lesson_plan_template.docx | |
| File Size: | 18 kb |
| File Type: | docx |
| 8.1_student_work.pdf | |
| File Size: | 1902 kb |
| File Type: | |
Reflection
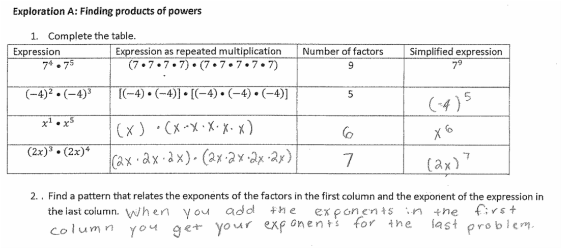
In the artifacts below, it is clear that the students were able to represent the expressions as repeated multiplication, as well as write the terms in their simplified forms. However, a misconception that needed to be cleared up was that (2x)^7 and (-4)^5 are not completely simplified. This misconception is addressed in Exploration 3, where students will need to combine like terms and further simplify the expressions (so instead of having (2x)^7, students would produce 2^7x^7).
It is also clear from the completion of the worksheets, and from discussions during the period, that students felt they were apart of developing these rules. By doing the repeated multiplication, when students have trouble remembering the rules, they can easily have a second approach (the repeated multiplication) to fall back on. Having multiple approach gives students more confidence, and keeps the students engaged throughout the period.
It is also clear from the completion of the worksheets, and from discussions during the period, that students felt they were apart of developing these rules. By doing the repeated multiplication, when students have trouble remembering the rules, they can easily have a second approach (the repeated multiplication) to fall back on. Having multiple approach gives students more confidence, and keeps the students engaged throughout the period.
After asking this student what they meant by "when you add up the expression you get your simplified expression is bigger," what he meant was when you count all of your like terms, you assign the power by how many terms there are, and this number will be bigger than the two original exponents. For example, you add up the number of x's in the repeated multiplication, you get 12, whereas in the original expression, it would appear as if there are only 6.
Overall, I was pleased with how this lesson went. I was originally worried that students would shun the repeated multiplication. However, most welcomed it and have continued to use this to remember what the powers of an expression mean. However, this method can be time-consuming and space-consuming. Although the repeated multiplication shows a great conceptual understanding of the properties of powers, I would like to see all students to move towards using the patterns, but still having the connections of the repeated multiplication in their prior knowledge. I was also very pleased with the level of engagement throughout the entirety of the hour, as well as the foundation that this format of assignment built for the remaining properties of exponents. Students felt comfortable approaching exponents with repeated multiplication for division properties and the zero and negative exponents.