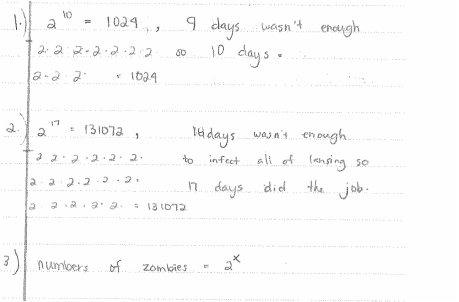Engaging and Motivating with Zombie Exponential Growth
This lesson, an introduction to the exponential growth model, was meant for students to explore the idea of assigning an equation to a particular situation. And what better way to motivate 9th graders than telling them their teacher has turned into a brain-hungry zombie?! I wrote a short newspaper article on a recent zombie outbreak at Michigan State, something that was particularly active amongst the math department. As a result, our classroom was being quarantined, and no students in the classroom were safe. As the video shows, the lesson was rather chaotic. However, the student work shows wonderful exploration into ways the zombie attack could be modeled with an equation. My goal for this lesson was for students to explore exponential growth. In later lessons, and during the unit review, this lesson was particularly useful to reference when talking about initial amounts, growth factors, and amount of time in the exponential growth model.
| zombie_attack_worksheet.docx | |
| File Size: | 16 kb |
| File Type: | docx |
| cs3_8.5_1st_hour_student_work.pdf | |
| File Size: | 929 kb |
| File Type: | |
| cs3_8.5_6th_hour_student_work.pdf | |
| File Size: | 1624 kb |
| File Type: | |
Reflection
This lesson taught me the importance of post-lesson reflection, especially when teaching the same lesson later on in the day. After completing the lesson with my 1st hour Algebra I class, I had spotted several confusing parts of the worksheet, and really tried to decide what my students actually got out of the lesson, other than a fun zombie re-enactment. My first hour did not move towards the generalization that is the the exponential growth model, as can be seen in several samples of student work. However, after reflecting and readjusting the questions and worksheet, my 6th hour students were much more successful in moving towards the generalization of the exponential growth model. Evidence of the changes made and the student responses are below.
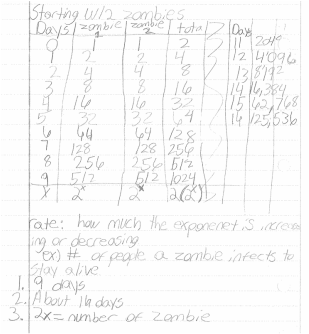
In the below sample of student work, the student misunderstood repeated multiplication of being able to multiply anything by 2. Although the information in the table is correct, he clearly does not have the understanding that the number of zombies increases much more quickly than if it were linear. This particular misconception was addressed with the students in the follow-up lesson.
In the below sample of student work, the student misunderstood repeated multiplication of being able to multiply anything by 2. Although the information in the table is correct, he clearly does not have the understanding that the number of zombies increases much more quickly than if it were linear. This particular misconception was addressed with the students in the follow-up lesson.
This student, also from the same hour, understood that the growth of zombies was exponential, but also did not represent the situation in a generalization. Since this was what I really wanted to see out of my students as understanding, I scrapped this worksheet (which I realized did not ask them to produce a generalization) and decided that 6th hour would produce an exit ticket that would ask them for a generalization of the exponential growth.
| 8.5_revised_exit_slip_wkst.docx | |
| File Size: | 229 kb |
| File Type: | docx |
The below student, from 6th hour, did the same thing as the student from 1st hour who correctly filled in their table, but represented the situation with a linear equation. This was easily cleared up by having the students actually use their rule, and seeing that it did not work. At this point, the students who did this realized that their equation was y=2^x, not y=2x.
This student used her knowledge of repeated multiplication, and using it to write an exponential equation, in order to produce an exponential growth model. This student clearly used her background knowledge gained from our previous work in finding patterns and writing equations in order to write her equation.
I was very pleased with the work the students did in exploring the exponential growth model. However, I was even more impressed by the enthusiasm they showed during the activity. Several students were able to produce the exponential growth model on their own, before the next lesson when everyone saw it in class. Because the students had experienced the model, those who had not produced it on their own more easily understood where the model came from, and were able to use it in different situations for assessments. Finally, I was very happy to see the amount of activities turned in on time, and the thought put into written responses. Before this activity, most requests for written responses were skipped over, whereas in this activity few students left these parts empty.